A very cranky old woman was arrested for shoplifting at a grocery store. She gave everyone a hard time, from the store manager to the security guard to the arresting officer who took her away. She complained and criticized everything and everyone throughout the process.Ha!
When she appeared before the judge, the judge asked her what she had stolen from the store. The lady defiantly replied, "Just a stupid can of peaches."The judge then asked why she had done it.
She replied, "I was hungry and forgot to bring any cash to the store.” The judge asked how many peaches were in the can.
She replied in a nasty tone, "Nine! But why do you care about that?”
The judge answered patiently, "Well, ma'am, because I'm going to give you nine days in jail -- one day for each peach.”
As the judge was about to drop his gavel, the lady's long-suffering husband raised his hand slowly and asked if he might speak. The judge said, "Yes sir, what do you have to add?”
The husband said meekly, "Your Honor, she also stole a can of peas.
Sunday, October 18, 2015
The cranky old lady...
The cranky old lady... Via my pistol-packing, Macified mom:
Twelve foot tall Cosmos!
Twelve foot tall Cosmos! My mom sends this photo, saying:
Special soil prepared by Scott, grown in 12 inch pot on my deck this summer...is 12 + high and just started to bloom. That is some nutritious soil! Warren is 6 feet tall.Scott is my brother, soon to be moving out here to Utah – and hopefully, to be providing said super-soil to us! Warren is my brother-in-law, who (when he's not gaping at giant Cosmos) is a great help to my mom by taking care of a zillion little (and some not so little) maintenance issues at her house.
Newspaper headlines...
Newspaper headlines... Reader Simi L. sent along a great collection of classic newspaper headlines. Many of them I'd seen before, but not these:
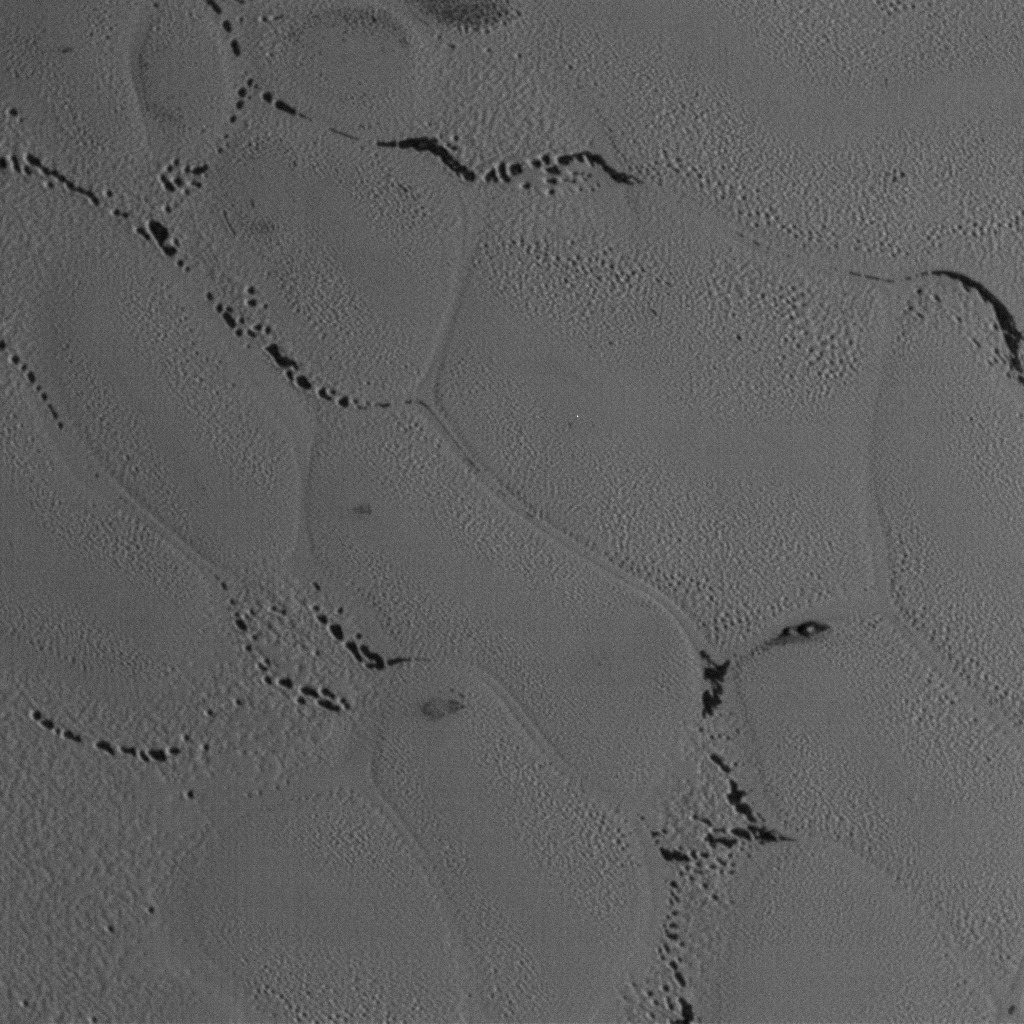
First findings released by New Horizons team...
First findings released by New Horizons team... Good article here. Lots of new raw photos, too, like the one of somewhere on Pluto at right. Pluto's surface is weird!
Mammatus clouds...
Mammatus clouds... The word “mammatus” is Latin for “having breasts”, which pretty much guarantees these are my favorite kind of cloud :) I've only seen them myself one time, in the Philippines when I was there in the U.S. Navy, in the '70s. Via APOD, of course...
Warthogs in Estonia...
Warthogs in Estonia... Gorgeous photos of American A-10 "Warthogs" parked under the aurora borealis at a military airfield (Ämari Air Base) not far from Tallinn, Estonia...
Paradise ponders...
Paradise ponders... It's raining today; started late yesterday afternoon in a stop-and-go kind of way. There hasn't been much accumulation out. The temperature is in the mid-50s, and it's 100% humidity (naturally), so it feels fairly chilly out even when it's not actually raining. It will be mostly an inside day today, I think. The dogs and I will have to live without our beloved morning walk.
I've been working away on a couple of tough (and therefore interesting) programming challenges. The first one is comparing the result of a double precision floating point with zero, where we want the result of the comparison to zero to be true even when the result of the subtraction is slightly different than zero. That's a far harder problem than one might think, a special variant of the also tough general case of simply comparing two floats. Click on the link to that article if you'd like to know more about the whys and wherefores.
I had an insight yesterday that led to a nice solution for me. In my original formulation, I did something like this:
The solution was crazy simple: I simply rewrote the formulation as:
The reason this solution worked is that epsilon is relative to the exponents of the numbers being compared. In the first formulation, if one or both a and b are computed and should be considered equal, there will likely be a very small difference between
The second issue I haven't solved yet. I need a hash function over an array that is sensitive to each nonzero value and its index. The function should generate different results if the values at a pair of indices are swapped, and should generate the same results no matter what order the values and indices happen to be presented in. I'm still pondering that one...
I've been working away on a couple of tough (and therefore interesting) programming challenges. The first one is comparing the result of a double precision floating point with zero, where we want the result of the comparison to zero to be true even when the result of the subtraction is slightly different than zero. That's a far harder problem than one might think, a special variant of the also tough general case of simply comparing two floats. Click on the link to that article if you'd like to know more about the whys and wherefores.
I had an insight yesterday that led to a nice solution for me. In my original formulation, I did something like this:
if( nearlyEqual( a - b, 0.0, epsilon ) {...}
Where a and b are doubles, and epsilon is how close a - b and 0.0 must be in order to be considered equal. This is a conventional comparison: you subtract the two numbers and compare the result to zero. In this case, however, the results can be wildly different than what you expected, as that linked article explains.The solution was crazy simple: I simply rewrote the formulation as:
if( nearlyEqual( a, b, epsilon ) {...}
Voila! No more problem. It always gives me a kick when I beat my head against the wall working on a tough problem, and the solution turns out to be easy!The reason this solution worked is that epsilon is relative to the exponents of the numbers being compared. In the first formulation, if one or both a and b are computed and should be considered equal, there will likely be a very small difference between
a - b – but exactly how small depends on the size of those numbers. In general, the exponent of the difference will be roughly 16 (base 10) less than the exponent of the given numbers. So if the two numbers were on the order of 10^100, the difference would be on the order of 10^84 – a tiny difference relative to the given numbers, but a long, long way from zero! So of course they don't look like they're nearly equal. In the second formulation, because a and b are the inputs to the nearlyEqual() function, the function knows what their exponents are, and can accurately judge what's close enough. Oh, so easy!The second issue I haven't solved yet. I need a hash function over an array that is sensitive to each nonzero value and its index. The function should generate different results if the values at a pair of indices are swapped, and should generate the same results no matter what order the values and indices happen to be presented in. I'm still pondering that one...